3.3 Positive Definite Matrices and Similar Matrices 阅读笔记
正定矩阵与相似矩阵
reference的内容为唯一教程, 接下来的内容仅为本人的课后感悟, 对他人或无法起到任何指导作用.
Reference
- Course website: Positive Definite Matrices and Minima | Linear Algebra | Mathematics | MIT OpenCourseWare and Similar Matrices and Jordan Form | Linear Algebra | Mathematics | MIT OpenCourseWare
- Course video: 【完整版-麻省理工-线性代数】全34讲 配套教材_哔哩哔哩_bilibili and 【完整版-麻省理工-线性代数】全34讲 配套教材_哔哩哔哩_bilibili
- Course summary: Lecture 27: Positive definite matrices and minima (mit.edu) and Lecture 28: Similar matrices and Jordan form (mit.edu)
本讲再次把重心放回实对称矩阵和正定性上. 正定还有什么几何意义呢? 我们引入二次型, 这是矩阵是否正定的真正定义. 二次型可以帮助我们判断 \(x^TAx\) 是否具有最小值, 椭圆和双曲线的部分跳过. 最后再探索正定矩阵的一些性质, 整个部分结束.
我们还会介绍相似矩阵, 相似矩阵其实就是不同基下面同一种线性变换. 后面的约当标准型跳过.
Test for Positive Definite
有矩阵 \(A=\begin{bmatrix}a&\cdots \\\vdots&\ddots\end{bmatrix}\), 判断其正定性有以下方法:
- All \(\lambda_i>0\)
- All sub-determinant \(> 0\)
- All pivot \(>0\)
- \(\bm{x}^{\mathrm{T}}A\bm{x}>0\) for \(\bm{x} \neq 0\)
大多数情况下使用 4 来定义正定性, 这个叫做二次型 (Quadratic Form). 而用前三条来验证正定性.
Quadratic Form and Minima
来计算一个例子: \(A=\begin{bmatrix}2&6\\6&?\end{bmatrix}\), 在 \(?\) 处填入多少才能使矩阵正定?
用前三条, 我们可以算出 \(?\) 部分如果小于 18, 则非正定. 等于 18, 为临界情况. 大于 18, 则正定.
1. 先看非正定, 把 7 带进去. 求二次型, 为 \(f(x_1,x_2)=2x_1^2+12x_1x_2+7x_2^2\). 在 \(x_1 = -x_2\) 处, 式子变为 \(-3x_2^{2}<0\). 从图上看是马鞍形, 有鞍点, 无极小值 (Minima).
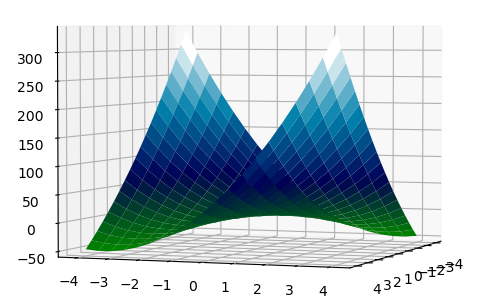
2. 再看正定, 把 20 带进去. 求二次型, 为 \(f(x_1,x_2)=2x_1^2+12x_1x_2+20x_2^2=2(x_1+3x_2)^{2}+2x_2^{2}\), 恒正. 在 \(x_1 = -3x_2\), \(x_2 = 0\) 处取极小值. 绘图:
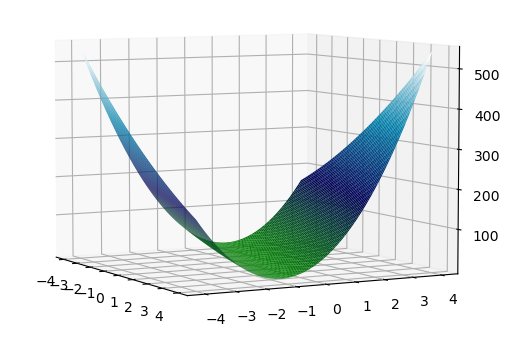
3. 来试试\(18\), 此时矩阵为 \(A=\begin{bmatrix}2&6\\6&18\end{bmatrix}\), \(\det A=0\), 此时的矩阵成为半正定矩阵 (Positive Semi-definite). 矩阵奇异, 其中一个特征值必为 \(0\), 从迹得知另一个特征值为 \(20\). 矩阵的主元只有一个, 为\(2\). 求二次型, 为 \(f(x_1,x_2)=2x_1^2+12x_1x_2+18x_2^2=2(x_1+3x_2)^{2}\). 在 \(x_1=-3x_2\) 处, 曲面贴着 \(0\), 无极小值.
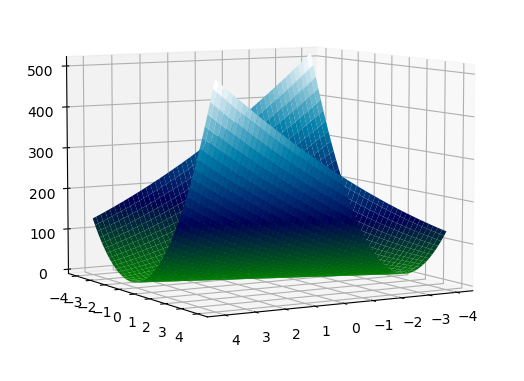
三个二次型表示的函数在 \(x_1=0, x_2=0\) 均有梯度为 0. 但是只有第二种有极小值. 一元函数, 如果 \(f'(x)=0\), \(f''(x)>0\), 则有极小值. 到了多元函数, 这可以用 Hessian 矩阵表示:
\[H_{f(x)} = \begin{bmatrix} f_{xx} & f_{xy} \\ f_{yx} & f_{yy} \\\end{bmatrix} \]当二阶偏导连续的时候, Hessian 矩阵为实对称的. 微积分说 Hessian 正定 + 一阶偏导为零对应极小值. 在这里二次型的矩阵 \(A=\begin{bmatrix}2&6\\6&18\end{bmatrix}\), 而 \(H_{f(x)}=\begin{bmatrix}4&12\\12&36\end{bmatrix}=2A\). 所以 Hessian 的正定性和二次型矩阵 \(A\) 的正定性是一样的. 可以直接用 \(A\) 的正定性判定最小值.
Properties of Positive Definite Matrices
最终提一点正定矩阵的性质, 证明简略:
-
\(A\) 正定, 则 \(A^{-1}\) 正定: \(A^{-1}=(S\Lambda S^{-1})^{-1}=S\Lambda^{-1}S^{-1}\), 所以 \(\lambda\) 变成倒数. 我们知道正定矩阵的特征值均为正值, 所以其逆矩阵的特征值也必为正值, 所以, 正定矩阵的逆矩阵也是正定的.
-
\(A,\ B\) 正定, 则 \(A+B\) 也正定: \(\bm{x}^{\mathrm{T}}(A+B)\bm{x}=\bm{x}^{\mathrm{T}}A \bm{x}+\bm{x}^{\mathrm{T}} B \bm{x}>0\). (\(\bm{x} \neq \boldsymbol{0}\))
-
对于 \(m\times n\) 的列满秩矩阵 \(A\), \(A^{\mathrm{T}}A\) 正定: 我们在投影部分经常使用\(A^{\mathrm{T}}A\), 这个运算会得到一个对称矩阵. $\bm{x}{\mathrm{T}}(A{\mathrm{T}}A) \bm{x}=(A \bm{x})^{\mathrm{T}}(A \bm{x})=\left\vert A \bm{x} \right\vert ^{2}\ge 0 $, 要保证模不为零, 则需要 \(A \bm{x}\) 的零空间中仅有零向量, 即 \(A\) 的各列线性无关, 这里满足.
-
正定矩阵具有良好的计算性质: 在矩阵数值计算中, 正定矩阵消元不需要进行"行交换"操作, 也不必担心主元过小或为零.
Similar Matrices
矩阵 \(A,\ B\) 对于某可逆矩阵 \(M\) 满足 \(B=M^{-1}AM\) 时, \(A,\ B\)互为相似矩阵, 记作 \(A\sim B\).
对于对角化中的式子 \(S^{-1}AS=\Lambda\), 则有\(A\sim \Lambda\).
联系前面基变换, 相似矩阵就是在不同基下面表示的同一种线性变换.
几何上我们会发现:
- 相似矩阵/不同基下同一种线性变换的特征值一样.
- 相似矩阵/不同基下同一种线性变换, 特征向量从一个基下面的坐标变道另一个.
证明:
已知 \(A \bm{x}=\lambda \bm{x},\ B=M^{-1}AM\).
根据数感学不会的, 化为 \(AMM^{-1}\bm{x}=\lambda x\).
接着两边同时左乘 \(M^{-1}\) 得 \(M^{-1}AMM^{-1}\bm{x}=\lambda M^{-1}\bm{x}\).
于是有 \(BM^{-1}\bm{x}=\lambda M^{-1}\bm{x}\).
特征值一样, 特征向量根据坐标变换公式. 原来特征向量是单位坐标系下的 \(\bm{x}\), 现在变换到 \(M\) 坐标系下表示的同一个向量的坐标了.
至此, 特征值和特征向量部分暂时告一段落, 下面将讲线代一个重要知识: 奇异值分解.