奇异值分解

reference的内容为唯一教程, 接下来的内容仅为本人的课后感悟, 对他人或无法起到任何指导作用.

Reference

1. Course website: Singular Value Decomposition | Linear Algebra | Mathematics | MIT OpenCourseWare
2. Course video: 【完整版-麻省理工-线性代数】全34讲 配套教材_哔哩哔哩_bilibili
3. Course summary: Lecture 29: Singular value decomposition (mit.edu)
4. Extra reading: 奇异值分解 SVD 原理与在降维中的应用 - 刘建平Pinard - 博客园 (cnblogs.com) and MIT—线性代数笔记 29 奇异值分解 - 知乎 (zhihu.com)

---

本讲内容为奇异值分解 (Singular Value Decomposition), 它适用于任何矩阵. 我没有深入学习, 在这一讲留下了两三个遗留问题.

奇异值分解是最好的一种矩阵分解. 任意一个矩阵 (任意 size, 不限方阵, 不限其他条件) 都可以写为:

\[A=U\Sigma V^{\mathrm{T}} \]

其中 \(A\) 是 \(m \times n\) 矩阵, \(U\), \(V\) 是 \(m \times m\) 和 \(n \times n\) 的正交矩阵. \(\Sigma\) 是 \(m \times n\) 的对角阵 (主对角线元素有值). 这一讲姑且假设 \(A\) 为方阵.

有几个跟 SVD 长得很像的形式:

• 当 \(A\) 为实对称矩阵时, \(A=Q\Lambda Q^{\mathrm{T}}\). 这是 SVD 的一种特殊情况.

• 当 \(A\) 可对角化时, \(A=S\Lambda S^{\mathrm{T}}\). 但是 \(S\) 并不是正交矩阵, 因此不属于 SVD.

假设我们已知任何矩阵都可以经如上形式的 SVD 分解.

How It Works

介绍具体求解方式之前, 先描述其意义.

很容易在 \(A\) 的行空间找到一组 orthonormal 的向量 (使用 Gram-Schmidt). 接下来经过线性变换 \(A\) 来到列空间, 设 \(\sigma_i \bm{u}_i = A \bm{v}_i\). 那么经过线性变换后的向量是否正交呢? 不一定, 需要特殊选择行空间的标准正交基.

用矩阵语言表述:

\[A \begin{bmatrix} \bm{v_1} & \cdots & \bm{v_r} \\\end{bmatrix} = \begin{bmatrix} \sigma_1 \bm{u_1} & \cdots & \sigma_r \bm{u_r} \\\end{bmatrix} \]

v 相互标准正交, u 相互标准正交. 我们的任务便是找到这样一组 u, v, 和 σ, 满足上面的式子.

此外零空间也可以找出一组标准正交的向量 \(\begin{bmatrix} \bm{v_{r+1}} & \cdots & \bm{v_n} \\\end{bmatrix}\), 如果想映射过去, 则 \(\sigma_i\) 为 0, 此时 \(\bm{u}\) 取什么都好, 但是我们需要找到一个正交矩阵 \(U\), 已经在列空间取了 r 个, 于是剩下的在左零空间取 m-r 个, 凑成 m 个标准正交向量.

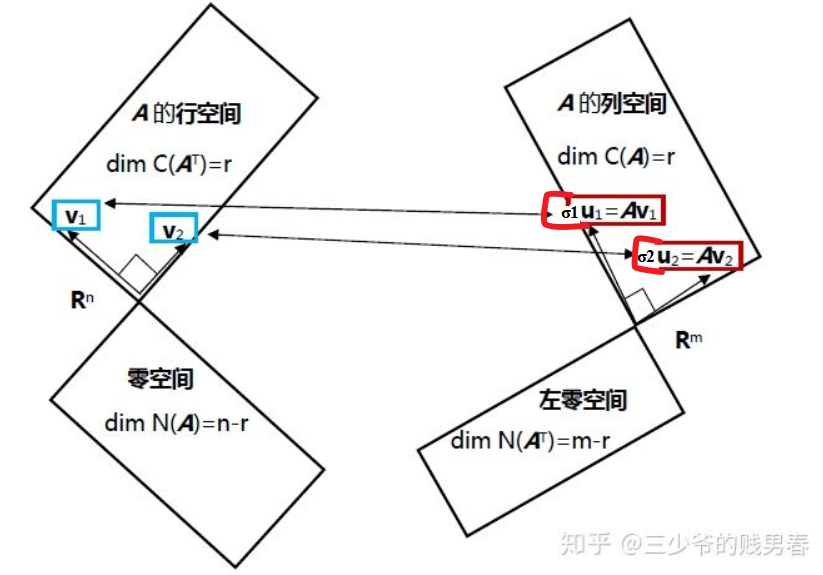
最终用矩阵语言描述为:

\[\begin{align*} AV &= A\Bigg[\bm{v}_1\ \bm{v}_2\ \cdots\ \bm{v}_r\ \bm{v}_{r+1}\ \cdots\ \bm{v}_m\Bigg] \\ &= \Bigg[\sigma_1\bm{u}_1\ \sigma_2\bm{u}_2\ \cdots\ \sigma_r\bm{u}_r\ 0\bm{u}_{r+1}\ \cdots\ 0\bm{u}_m\Bigg]\\ &= \Bigg[\bm{u}_1\ \bm{u}_2\ \cdots\ \bm{u}_r\ \bm{u}_{r+1}\ \cdots \ \bm{u}_n\Bigg]\left[\begin{array}{c c c|c}\sigma_1&&&\\&\ddots&&\\&&\sigma_r&\\\hline&&&\begin{bmatrix}0\end{bmatrix}\end{array}\right]\\ &= U \Sigma \end{align*} \]

此时 \(U\) 是 \(m\times m\) 正交矩阵, \(\Sigma\) 是 \(m\times n\) 对角矩阵, \(V^{\mathrm{T}}\) 是 \(n\times n\) 正交矩阵.

最终可以写为 \(AV=U\Sigma\), 进一步可以写作 \(A=U\Sigma V^{-1}\), 因为 \(V\) 是标准正交矩阵所以可以写为 \(A=U\Sigma V^{\mathrm{T}}\).

我们的任务便是找到这样一组 u, v, 和 σ, 满足上面的式子. 此时仍然假设我们已知任何矩阵都可以经如上形式的 SVD 分解.

How to Find \(U\), \(V\), and \(\Sigma\)?

如果已知任何矩阵都可以经如上形式的 SVD 分解: \(A=U\Sigma V^{\mathrm{T}}\).

则 \(A^{\mathrm{T}}A = V \Sigma^{\mathrm{T}} U^{\mathrm{T}}U \Sigma V^{\mathrm{T}} = V \Sigma^{\mathrm{T}}\Sigma V^{\mathrm{T}}=V \Sigma'^{2}V^{\mathrm{T}}\).

这里 \(\Sigma\) 不是方阵, 但是转置乘自身, 最终仍然会得到一个对角阵. (有的元素可能是零).

同理有 \(AA^{\mathrm{T}} = U\Sigma\Sigma^{\mathrm{T}}U^{\mathrm{T}}=U\Sigma''^{\mathrm{T}}U^{\mathrm{T}}\).

假设 \(A\) 行满秩, 列也满秩 (满秩方阵), 那么 \(A A^{\mathrm{T}}\) 和 \(A^{\mathrm{T}} A\) 全都是实对称正定矩阵.

• \(A^{\mathrm{T}} A\) 的特征值满足 \(\sigma_i=\sqrt{\lambda_i}\), 特征向量组成正交矩阵 \(V\).
• \(A A^{\mathrm{T}}\) 的特征值满足 \(\sigma_i=\sqrt{\lambda_i}\), 特征向量组成正交矩阵 \(U\).

Example

Invertible

计算一个例子, \(A=\begin{bmatrix}4&4\\-3&3\end{bmatrix}\), 我们需要找到:

我们来计算 \(A^{\mathrm{T}}A=\begin{bmatrix}4&-3\\4&3\end{bmatrix}\begin{bmatrix}4&4\\-3&3\end{bmatrix}=\begin{bmatrix}25&7\\7&25\end{bmatrix}\).

可以直接观察得到特征向量 \(A^{\mathrm{T}}A\begin{bmatrix}1\\1\end{bmatrix}=32\begin{bmatrix}1\\1\end{bmatrix},\ A^{\mathrm{T}}A\begin{bmatrix}1\\-1\end{bmatrix}=18\begin{bmatrix}1\\-1\end{bmatrix}\), 化为单位向量有 \(\sigma_1=32,\ \bm{v}_1=\begin{bmatrix}\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}\end{bmatrix},\ \sigma_2=18,\ \bm{v}_2=\begin{bmatrix}\frac{1}{\sqrt{2}}\\-\frac{1}{\sqrt{2}}\end{bmatrix}\).

到目前为止, 我们得到 \(\begin{bmatrix}4&4\\-3&3\end{bmatrix}=\begin{bmatrix}u_?&u_?\\u_?&u_?\end{bmatrix}\begin{bmatrix}\sqrt{32}&0\\0&\sqrt{18}\end{bmatrix}\begin{bmatrix}\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}\end{bmatrix}\), 接下来继续求解 \(U\).

\(AA^{\mathrm{T}}=U\Sigma V^{\mathrm{T}}V\Sigma^{\mathrm{T}}U^{\mathrm{T}}=U\Sigma^2U^{\mathrm{T}}\), 求出 \(AA^{\mathrm{T}}\) 的特征向量即可得到 \(U\), \(\begin{bmatrix}4&4\\-3&3\end{bmatrix}\begin{bmatrix}4&-3\\4&3\end{bmatrix}=\begin{bmatrix}32&0\\0&18\end{bmatrix}\), 观察得 \(AA^{\mathrm{T}}\begin{bmatrix}1\\0\end{bmatrix}=32\begin{bmatrix}1\\0\end{bmatrix},\ AA^{\mathrm{T}}\begin{bmatrix}0\\1\end{bmatrix}=18\begin{bmatrix}0\\1\end{bmatrix}\). 但是我们不能直接使用这一组特征向量, 因为式子 \(AV=U\Sigma\) 明确告诉我们, 一旦\(V\)确定下来, \(U\)也必须取能够满足该式的向量, 所以此处 \(\bm{Av}_2=\begin{bmatrix}0\\-\sqrt{18}\end{bmatrix}=\bm{u}_2\sigma_2=\begin{bmatrix}0\\-1\end{bmatrix}\sqrt{18}\), 则 \(\bm{u}_1=\begin{bmatrix}1\\0\end{bmatrix},\ \bm{u}_2=\begin{bmatrix}0\\-1\end{bmatrix}\). (这个问题在本讲的官方笔记中有详细说明. )

如果取 \(\bm{v}_2=\begin{bmatrix}-\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}\end{bmatrix}\), 则可以取 \(\bm{u}_1=\begin{bmatrix} 1 \\ 0 \\\end{bmatrix}, \bm{u}_2=\begin{bmatrix} 0 \\ 1 \\\end{bmatrix}\).

\(U\) 和 \(V\) 是相关的, 标准正交基到底该怎么取呢? 这又是一个问题.

Singular

再做一个例子, \(A=\begin{bmatrix}4&3\\8&6\end{bmatrix}\), 这是个秩一矩阵, 有零空间.

我们按照最初的原理去看行列空间. \(A\) 的行空间为 \(\begin{bmatrix}4\\3\end{bmatrix}\) 的倍数, \(A\) 的列空间为 \(\begin{bmatrix}4\\8\end{bmatrix}\) 的倍数.

标准化向量得 \(\bm{v}_1=\begin{bmatrix}0.8\\0.6\end{bmatrix},\ \bm{u}_1=\frac{1}{\sqrt{5}}\begin{bmatrix}1\\2\end{bmatrix}\).

\(A^{\mathrm{T}}A=\begin{bmatrix}4&8\\3&6\end{bmatrix}\begin{bmatrix}4&3\\8&6\end{bmatrix}=\begin{bmatrix}80&60\\60&45\end{bmatrix}\), 由于 \(A\) 是秩一矩阵, 则 \(A^{\mathrm{T}}A\) 也不满秩, 所以必有特征值 \(0\), 则另特征值一个由迹可知为 \(125\).

继续求零空间的特征向量, 有 \(\bm{v}_2=\begin{bmatrix}0.6\\-0,8\end{bmatrix},\ \bm{u}_2=\frac{1}{\sqrt{5}}\begin{bmatrix}2\\-1\end{bmatrix}\).

最终得到\(\begin{bmatrix}4&3\\8&6\end{bmatrix}=\displaystyle \frac{1}{\sqrt{5}}\begin{bmatrix}1&\bm{2}\\2&\bm{-1}\end{bmatrix}\begin{bmatrix}\sqrt{125}&0\\0&\bm{0}\end{bmatrix}\begin{bmatrix}0.8&0.6\\\bm{0.6}&\bm{-0.8}\end{bmatrix}\), 其中加粗部分都是与零空间相关的部分.

最终得出 SVD 的结论:

• \(\bm{v}_1,\ \cdots,\ \bm{v}_r\) 是行空间的标准正交基
• \(\bm{u}_1,\ \cdots,\ \bm{u}_r\) 是列空间的标准正交基
• \(\bm{v}_{r+1},\ \cdots,\ \bm{v}_n\) 是零空间的标准正交基
• \(\bm{u}_{r+1},\ \cdots,\ \bm{u}_m\) 是左零空间的标准正交基

通过将矩阵写为\(Av_i=\sigma_iu_i\)形式, 将矩阵对角化, 便可以得到 SVD 分解.

Question Unsolved

目前仍有很多问题:

• 为什么矩阵 \(A\) 一定能分解为 \(U \Sigma V^{\mathrm{T}}\)?
• 既然 \(U\) 和 \(V\) 是有联系的, 怎么选特征向量的方向, 怎么求?
• 第二个例子能否采用求 \(A^{\mathrm{T}}A\) 和 \(A A^{\mathrm{T}}\) 的特征值特征向量算出 SVD?
• 非满秩的矩阵的 SVD, 算出 \(\sigma_i=0\) 对应的零空间/左零空间的向量有意义吗?
• SVD 本身是用来做什么的?

Properties and Applications

这一部分直接截图别人写的了:

Properties

上面几节我们对SVD的定义和计算做了详细的描述，似乎看不出我们费这么大的力气做SVD有什么好处。那么SVD有什么重要的性质值得我们注意呢？

对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说：

\[\begin{align*} A_{m×n}&=U_{m×m}\Sigma_{m×n}V^{\mathrm{T}}_{n×n}\\ &≈U_{m×k}\Sigma_{k×k}V^{\mathrm{T}}_{k×n}A_{m×n}\\ &=U_{m×m}Σ_{m×n}V_{n×n}^{\mathrm{T}}\\ &≈U_{m×k}Σ_{k×k}V_{k×n}^{\mathrm{T}}\\ \end{align*} \]

其中 \(k\) 要比 \(n\) 小很多，也就是一个大的矩阵 \(A\) 可以用三个小的矩阵 \(U_{m×k}\), \(\Sigma_{k×k}\), \(V^{\mathrm{T}}_{k \times n}\) 来表示。如下图所示，现在我们的矩阵 \(A\) 只需要灰色的部分的三个小矩阵就可以近似描述了。

由于这个重要的性质，SVD 可以用于 PCA 降维，来做数据压缩和去噪。也可以用于推荐算法，将用户和喜好对应的矩阵做特征分解，进而得到隐含的用户需求来做推荐。同时也可以用于 NLP 中的算法，比如潜在语义索引（LSI）。下面我们就对 SVD 用于 PCA 降维做一个介绍。

Application: PCA

在主成分分析（PCA）原理总结中，我们讲到要用PCA降维，需要找到样本协方差矩阵 \(X^{\mathrm{T}}X\) 的最大的d个特征向量，然后用这最大的d个特征向量张成的矩阵来做低维投影降维。可以看出，在这个过程中需要先求出协方差矩阵 \(X^{\mathrm{T}}X\)，当样本数多样本特征数也多的时候，这个计算量是很大的。

注意到我们的SVD也可以得到协方差矩阵 \(X^{\mathrm{T}}X\) 最大的d个特征向量张成的矩阵，但是SVD有个好处，有一些SVD的实现算法可以不求先求出协方差矩阵 \(X^{\mathrm{T}}X\)，也能求出我们的右奇异矩阵V。也就是说，我们的PCA算法可以不用做特征分解，而是做SVD来完成。这个方法在样本量很大的时候很有效。实际上，scikit-learn的PCA算法的背后真正的实现就是用的SVD，而不是我们我们认为的暴力特征分解。

另一方面，注意到PCA仅仅使用了我们SVD的右奇异矩阵，没有使用左奇异矩阵，那么左奇异矩阵有什么用呢？