有四个人夜间过一座独木桥，他们只有一只手电筒．而这座独木桥一次最多允许两人同时通过，而过桥的时候必须持有手电筒，所以就得有人把手电筒带来带去．两人同行时以较慢者的速度为准，四人过桥时间分别是1分、2分、5分和10分．他们四人过完桥最少需要17 分钟．

2

分析与解答揭秘难题真相，上天天练！

习题“有四个人夜间过一座独木桥，他们只有一只手电筒．而这座独木桥一次最多允许两人同时通过，而过桥的时候必须持有手电筒，所以就得有人把手电筒带来带去．两人同行时以较慢者的速度为准，四人过桥时间分别是1分、2分、5分和1...”的分析与解答如下所示：

分析 根据要求出四个人过桥最少时间，即可得出应首先让用时最少的两人先过桥，让他们往返送灯会节省时间，进而分别分析得出即可． 解答 根据要求出四个人过桥最少时间，即可得出应首先让用时最少的两人先过桥，让他们往返送灯会节省时间，
故：（1）1分钟的和2分钟的先过桥（此时耗时2分钟）． 
（2）1分钟的回来，（此时共耗时3分钟）． 
（3）5分钟的和10分钟的过桥（共耗时2+1+10=13分钟）． 
（4）2分钟的回来（共耗时2+1+10+2=15分钟）． 
（5）1分钟的和2分钟的过桥（共耗时2+1+10+2+2=17分钟）． 
此时全部过桥，共耗时17分钟． 
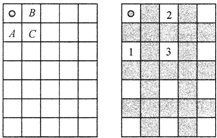
故答案为：17． 点评 此题主要考查了应用类问题，结合实际发现用时最少的两人先过桥往返送灯会节省时间是解题关键． 融会贯通找提分点，上天天练！ 与“有四个人夜间过一座独木桥，他们只有一只手电筒．而这座独木桥一次最多允许两人同时通过，而过桥的时候必须持有手电筒，所以就得有人把手电筒带来带去．两人同行时以较慢者的速度为准，四人过桥时间分别是1分、2分、5分和1...”相似的题目： 有15枚棋子，甲、乙两人轮流取，每次只能取1～2枚但不能不取，谁取到最后一枚棋子谁就获胜．甲怎么才能获胜？      看答案   加收藏 盒子里放着200枚棋子，甲、乙两人轮流取，甲先乙后，每人每次可取1～3枚，谁取得最后一枚谁获胜．谁能必胜，请说出必胜的策略．      看答案   加收藏 图是一个5×7的方格棋盘，左上角有1枚棋子．甲先乙后，两人轮流走这枚棋子，每人每次只能向下、向右或向右下走一格，如图中棋子可以走A、B、C三格之一．谁将棋子走入右下角方格中谁获胜．如果都按最佳方法走，那么谁将获胜？怎样走？     

 

---

商场里买100元的东西会返80元代金元实际折扣是多少？0

相当于100元当成150元用，也就是150元的东西100元就可以买下来了，折扣就是100/150=67%， 

应该是100÷（100+50）=0.666666666折

---

能不能不要太多？25匹马赛跑问题新解

 海蚀我心 2015-11-07 09:27:06 题目：25匹马赛跑，每次只能跑5匹马，最快能赛几次找出跑得最快的3匹马？赛跑不能计时，并假设每匹马的速度是恒定不变的。答案，过程。
我从网上搜到答案，最少7场：
前5次分出五组中每组的排名，第6次为每组第一名比赛，得到25匹中最快的马，并按5匹马排名排列分组，得：
A：1，2，3，4，5
B：1，2，3，4，5
C：1，2，3，4，5
D：1，2，3，4，5
E：1，2，3，4，5
A1为最快的马；
从第6次比赛可排除D、E两组（D、E中最快的比A1、B1、C1慢，故不可能进前3），同理排除A组的4、5名，B组的3、4、5名，C组的2、3、4、5名，所以参加第7次的只剩下A2、A3、B1、B2、C1
第7次可决出第2、3名
综上，共需7场比赛


我的解答与原解答有一点关键的区别：题设中跑道可以同时让五匹马赛跑，换句话说，从出发点只能有五匹马出发，但是将终点作为新的出发点，即可令十匹马一起赛跑，这是毫无疑问的，并不影响同时令五匹进行比赛的本质。
Q：那么将这十匹马作为A组，怎么决出前三名呢？
A：令两边的赛马同时赛跑，相向而行，左边五匹马必定和右边五匹马依次相遇在赛道的5*5=25个点，考虑前三次相遇。
显而易见，首先左边的第一和右边的第一会第一次相遇，时间相同的情况下比较路程，此时只要观察两匹马相遇时和原出发点的距离，就能够知道哪匹马是这一组中的第一名。
假设左一为A1（A1为最快的马），那么右一和左二会第二次相遇，同理可得A2，假设右一为A2，最后左二和右二第三次相遇，同理可得A3.这是因为每次决出第一之后，就不用再管第一了，我所举的例子里左二会直接递补左一的空位，也就是说每次都是左一和右一比较，但现在A1的名额满了，A2还空着，第二次相遇会占住A2的名额，第三次占住A3，依次类推。

第一场取A：A1、A2、A3；
第二场对B组同样处理，B：B1、B2、B3；
A组、B组与C组共（3+3）+5=6+5=11匹，超过一场比赛的10匹马上限。
这里需要一点点小技巧，A组取A1和A2，A3暂不取，将A1、A2、B1、B2、B3与C组五匹马放在第三场决出前三。
判断是否需要跑第四场的条件O：当且仅当A1为这24匹马中第一名，A2为这24匹马中第二名
时，这时需将少跑一场的A3与第三场中的第三名单独跑第四场。这是因为25匹马中第三名有可能在原来第一、第二名所在组里。
当然A1、A2刚好是24匹马中的第一和第二的概率并不是特别高，换句话说我们很有可能跑三场就够了。

跑第四场的概率劳烦对这个问题有兴趣的计算一下。我对这个不是很懂。
怕算错了，丢脸。。。    

---

【智力问题】25匹马赛跑，每次只能跑5匹马，最快能赛几次找出跑得最快的3匹马？赛跑不能计时，并假设每匹马的速度是恒定不变的。

 

答案是7次。

1. 首先将25匹马分成5组a、b、c、d、e进行比赛。比赛的次数就是5次。得到每组的第一名，分别编号a1,b1,c1,d1,e1。

2. 然后我们将每组的第一名进行比赛，得出结果。假设a1>b1>c1>d1>e1。（大于号表示a1比b1快，1表示第一名）。在这个地方我们可以推断出，a1是所有马中最快的，所以它是第一名。d1,e1不可能是前三的马，同时这两匹马所在的组也不可能是前三的马。所以排除这两组马，还剩三组15匹马。现在需要找出第二快和第三快的马。

3. 第二名和第三名的马在刚才的比赛中有以下几种分布情况：

　　全部在a组（最快的马所在的组），那么它有是a1和a3.

　　全部在b组，那么它们就是b1和b2。

　　一匹在a组一匹在b组，那么它们是a2和b1.无论是第三名在a组还是第二名在a组都是这两匹。

　　一匹在a组一匹在c组，那么它们是a2和c1。

　　一匹在b组一匹在c组，那么它们是b1和c1。

　　所以我们把a2,a3,b1,b2,c1拿出来再进行一场比赛。取前两名就是最终的结果。