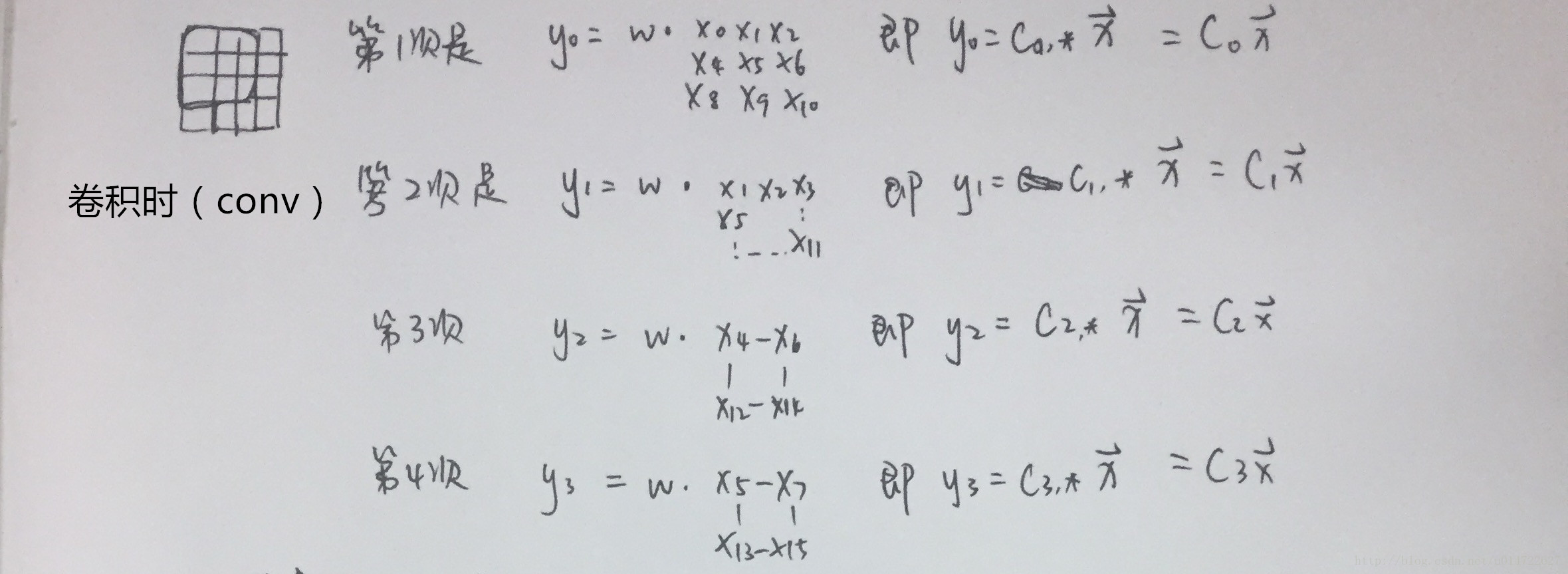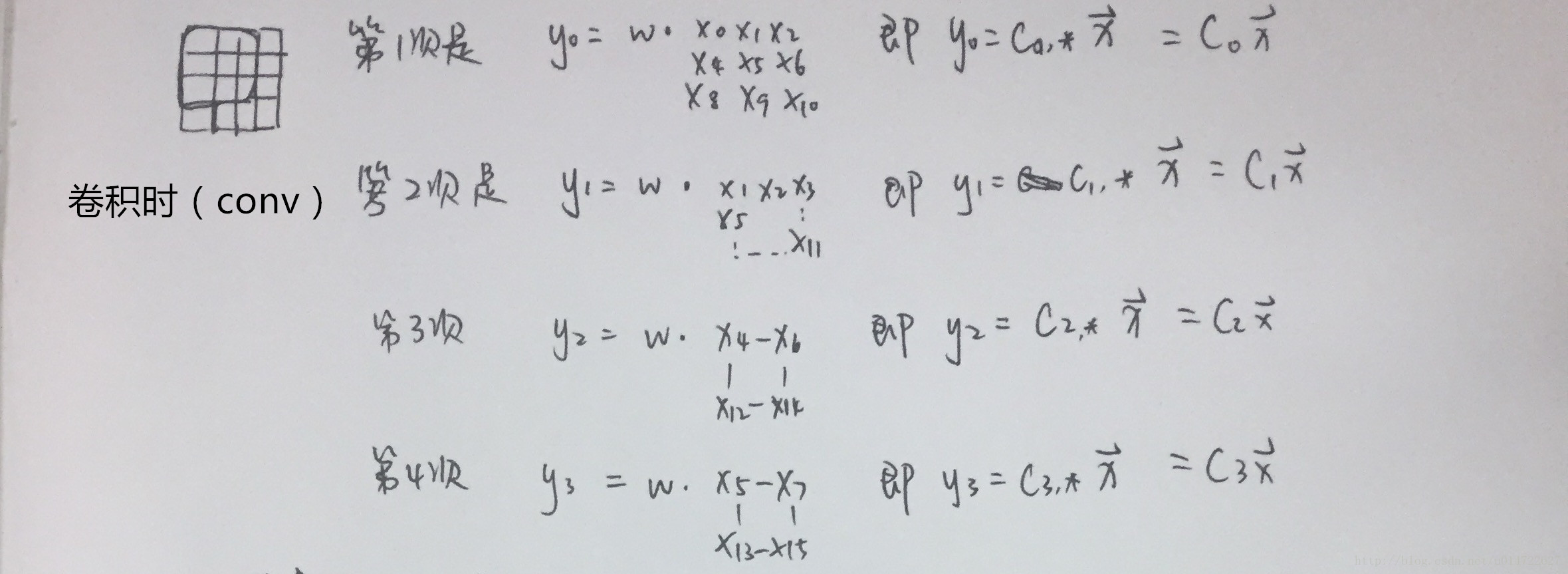深度学习卷积网络中反卷积/转置卷积的理解 transposed conv/deconv

搞明白了卷积网络中所谓deconv到底是个什么东西后，不写下来怕又忘记，根据参考资料，加上我自己的理解，记录在这篇博客里。

1）

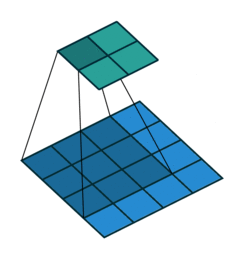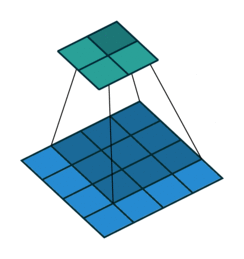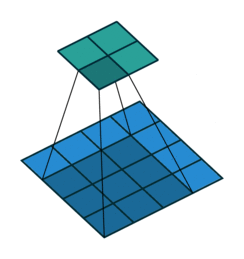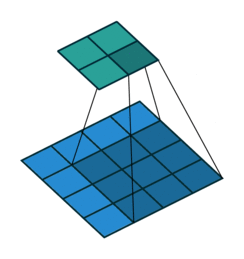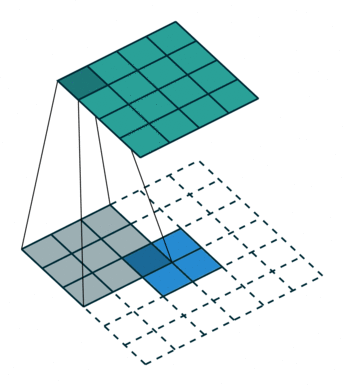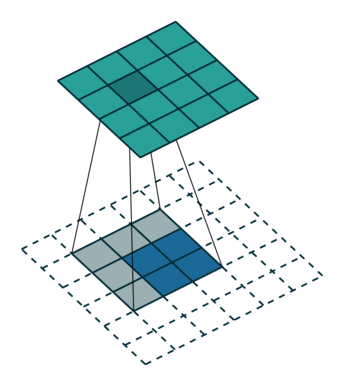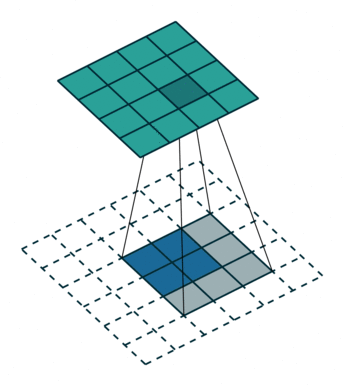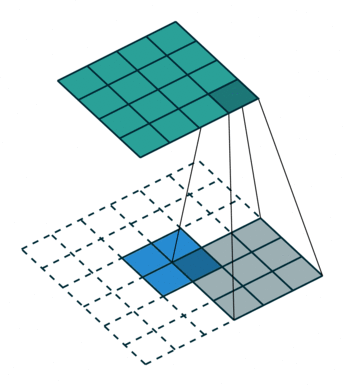卷积  i=4,k=3,p=0,s=1,则 o=2"> i=4,k=3,p=0,s=1,则 o=2$i=4,k=3,p=0,s=1,则o=2$	反卷积 i=2,k=3,p=0,s=1,则 o=4"> i=2,k=3,p=0,s=1,则 o=4$i=2,k=3,p=0,s=1,则o=4$

注意图中蓝色（下面）是输入，绿色（上面）是输出，卷积和反卷积在 p、s、k "> p、s、k $p、s、k$等参数一样时，是相当于 i"> i$i$ 和 o"> o$o$ 调了个位。 
这里说明了反卷积的时候，是有补0的，即使人家管这叫no padding（ p=0"> p=0$p=0$），这是因为卷积的时候从蓝色 4×4"> 4×4$4\times 4$ 缩小为绿色 2×2"> 2×2$2\times 2$，所以对应的 p=0"> p=0$p=0$ 反卷积应该从蓝色 2×2"> 2×2$2\times 2$ 扩展成绿色 4×4"> 4×4$4\times 4$。而且转置并不是指这个 3×3"> 3×3$3\times 3$ 的核 w"> w$w$ 变为 wT"> wT$w^T$，但如果将卷积计算写成矩阵乘法（在程序中，为了提高卷积操作的效率，就可以这么干，比如tensorflow中就是这种实现）， Y→=CX→"> Y? =CX? $\overrightarrow{Y}=C\overrightarrow{X}$（其中 Y→"> Y? $\overrightarrow{Y}$ 表示将 Y→"> Y? $\overrightarrow{Y}$ 拉成一维向量， X→"> X? $\overrightarrow{X}$ 同理），那么反卷积确实可以表示为 CTY→"> CTY? $C^T\overrightarrow{Y}$，而这样的矩阵乘法，恰恰等于 w"> w$w$ 左右翻转再上下翻转后与补0的 Y"> Y$Y$卷积的情况。

然后就产生了第三个confuse：“补0了会不会有影响，还能通过反卷积近似输入 X"> X$X$ 吗？”其实反卷积也不一定能达到近似的效果，图像里的卷积，相当于一种相关操作，而反卷积维持了这种相关操作时的 w"> w$w$ 与 X"> X$X$、与 Y"> Y$Y$ 之间的联系维持了。至于补0后操作是否还等价，上一段已经说明了是等价的，读者可以在阅读完后面的文章后自己尝试一下。

---

2写的非常详细，还有很多例子便于理解，在这里我就截图出重点来（ps.文中的figure2.1就是上图的左边）。剩下的例子请大家多看看原文，最好自己动手算一下，我也贴个我算的过程（ Ci"> Ci$C_i$ 表示矩阵 C"> C$C$ 的第 i"> i$i$ 行），供参考。 
关于反向传播， 知乎-如何理解深度学习中的deconvolution networks3有详细的推导过程。